С древности считалось, что небесные тела двигаются по «идеальным кривым» — окружностям. В теории Коперника также предполагалось круговое движение. Однако в XVII веке стало ясно, что орбиты небесных тел отличаются от окружностей. Это важное открытие принадлежит Иоганну Кеплеру. Кеплер не подвергал сомнению основные положения учения Коперника, но заметил расхождения между предварительно рассчитанными и наблюдаемыми положениями планет. Чтобы устранить это несоответствие, Кеплеру пришлось отойти от кругового и равномерного движения планет. Для определения гелиоцентрических орбит он использовал данные наблюдений датского астронома Тихо Браге. Особенно внимательно Кеплер изучил движение Марса. В результате многолетних исследований он сформулировал три основных закона движения планет, получивших его имя.
1. Первый закон Кеплера утверждает, что орбита каждой планеты представляет собой эллипс, в одном из фокусов которого находится Солнце. Форма эллипса характеризуется эксцентриситетом (e), который выражается как отношение расстояния от центра эллипса до фокуса (c) к большой полуоси (a). Если c = 0 (фокус совпадает с центром), то e = 0 и эллипс превращается в окружность радиусом a. Большинство планет имеют орбиты, близкие к окружностям, с небольшими значениями эксцентриситета. Например, эксцентриситет орбиты Земли составляет 0,0167.
Ближайшая к Солнцу точка орбиты называется перигелием, а наиболее удаленная — афелием. Большая полуось орбиты планеты представляет ее среднее расстояние от Солнца и используется как астрономическая единица (а.е.). Одна астрономическая единица равна примерно 149 600 000 км.
Помимо планет, по эллипсам движутся и их естественные и искусственные спутники. Ближайшая к Земле точка орбиты Луны или спутников называется перигеем, а наиболее удаленная — апогеем.
2. Второй закон Кеплера утверждает, что радиус-вектор планеты описывает равные площади за равные промежутки времени. Это означает, что когда планета движется по своей орбите, скорость ее изменяется так, чтобы площадь, заметаемая радиус-вектором, была одинаковой для равных интервалов времени.
3. Третий закон Кеплера утверждает, что квадраты сидерических периодов обращения двух планет относятся как кубы больших полуосей их орбит. Если большие полуоси орбит двух планет обозначаются как a₁ и a₂, а периоды обращений как T₁ и T₂, то третий закон Кеплера можно записать в виде:
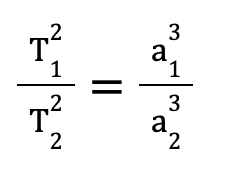
Этот закон применим не только к движению планет, но и к движению их естественных и искусственных спутников.
Пример 4. За какое время Марс, находящийся от Солнца примерно в полтора раза дальше, чем Земля, совершает полный оборот вокруг Солнца?
Если Марс находится от Солнца примерно в полтора раза дальше, чем Земля, и обозначим расстояния как a₁ (для Земли) и a₂ (для Марса), то период обращения Марса (T₂) можно найти, используя третий закон Кеплера:
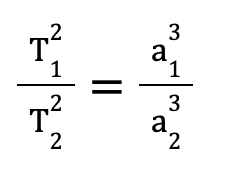
Дано, что a₂ = 1.5 * a₁. Подставим это значение:
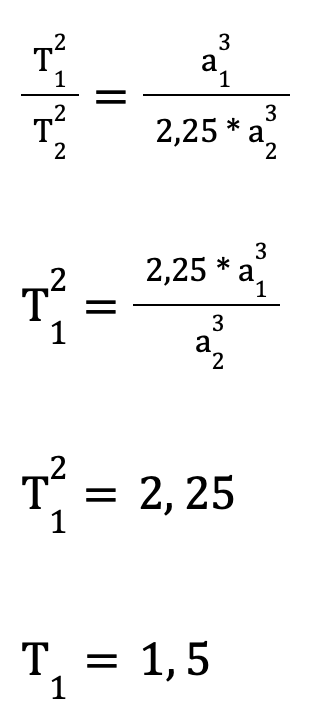
Так как период обращения Земли (T₁) равен примерно 1 году, период обращения Марса (T₂) составит 1.5 года.













