В астрономии существовало представление о «сфере неподвижных звезд» не только в геоцентрической, но и в гелиоцентрической системе мира. Считалось, что звезды действительно расположены на шаровой поверхности, то есть все они отстоят от нас на одном и том же расстоянии и не двигаются относительно друг друга. Данный и следующие параграфы позволят убедиться в ошибочности этих представлений.
1. Определение расстояний до звезд. Для измерения расстояний до ближайших звезд применяется метод параллакса, который также эффективен в измерениях расстояний до тел Солнечной системы. Однако в данном случае базисом служит не радиус Земли, а средний радиус земной орбиты.
Угол (π), под которым со звезды был бы виден средний радиус земной орбиты (а), расположенный перпендикулярно направлению на звезду, называется годичным параллаксом. В тех случаях, когда удается определить значение π, расстояние до звезды (r) вычисляется по формуле:
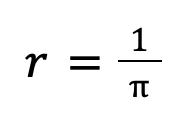
Угол (π) всегда очень мал (меньше 1 угловой секунды). Поэтому формулу можно записать в виде:
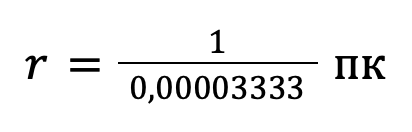
Расстояние до звезды, которое соответствует параллаксу в 1 угловой секунде, называется парсеком (обозначается пк):
1пк=206265а.е.
Эта единица используется в звездной астрономии, так как не только километр, но и даже астрономическая единица (а. е.) слишком мала для измерения расстояний до звезд. Очевидно, что расстояние до звезды в парсеках легко вычислить по формуле:
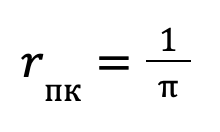
Самая близкая к нам звезда (не считая Солнца!) находится в созвездии Центавра (Проксима Центавра или Кентавра). Ее годичный параллакс составляет 0,76 угловых секунд. Менее чем полтора века назад астрономам, в том числе астроному Пулковской обсерватории В. Я. Струве (1793 — 1864), удалось впервые определить расстояние до звезды Вега. Сейчас уже известны параллаксы нескольких тысяч звезд.
Давайте выясним, сколько километров содержится в парсеке, а также найдем соотношение между парсеком и световым годом, расстоянием, которое свет проходит за год (обозначается св. г., св. лет). Поскольку 1 а. е. = 1,496 * 108 км, то:
1пк=206265а.е.=206265∙1,496∙108км=3,08∙1013км.1пк=206265а.е.=206265∙1,496∙108км=3,08∙1013км.
1св.г.=3∙105км/с∙365,25∙24∙3600с=9,46∙1012км.св.лет.1св.г.=3∙105км/с∙365,25∙24∙3600с=9,46∙1012км.св.лет.
103пк=1кпк(килопарсек);106пк=1Мпк(мегапарсек).103пк=1кпк(килопарсек);106пк=1Мпк(мегапарсек).
Пример 7. Годичный параллакс Веги (а Лиры) равен 0,12 угловых секунд. Каково расстояние до нее в парсеках и световых годах?
Для расчета расстояния до звезды по её годичному параллаксу можно использовать формулу:
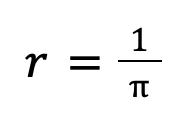
где:
- r — расстояние до звезды в парсеках,
- π — годичный параллакс в угловых секундах.
Для Веги (aa-Лиры) с годичным параллаксом в 0,12˝:
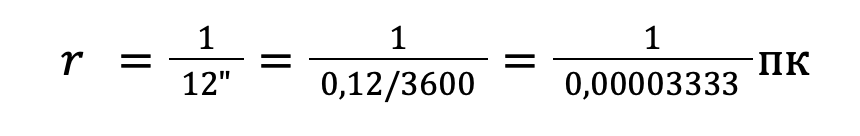
Теперь, чтобы перевести расстояние в световые годы (св. лет), мы знаем, что 1 световой год равен примерно 9,46×10¹² километров. Таким образом:
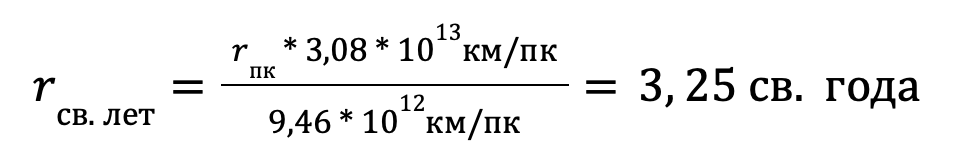
Итак, расстояние до Веги составляет приблизительно 3,25 световых года.













