1. Определение расстояний по параллаксам светил. Для измерения расстояний до недоступных точек используется метод параллаксов, который основан на треугольниках. Допустим, нужно определить расстояние от точки А до недоступной точки С. Сначала измеряется расстояние до какой-то доступной точки В, что создает базис АВ. Затем с помощью угломерного геодезического инструмента измеряются углы CAB и АВС. После этого, используя тригонометрические формулы, можно вычислить оставшиеся элементы треугольника ABC.
Параллакс — это угол, под которым наблюдается базис из недоступной точки. При фиксированном расстоянии до объекта, параллакс увеличивается с увеличением базиса.
Внутри Солнечной системы часто используется экваториальный радиус Земли как базис. Наблюдатель видит светило на горизонте под углом р0. Горизонтальный экваториальный параллакс — это угол, под которым экваториальный радиус Земли был бы виден из точки на горизонте, где находится светило. Этот параметр измеряется через наблюдения высоты светила в момент верхней кульминации из двух точек на земной поверхности с известными географическими широтами.
Если известен горизонтальный параллакс (р0), то расстояние до светила можно вычислить по формуле:
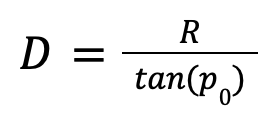
Где:
- D — расстояние от центра Земли до центра небесного тела
- R — экваториальный радиус Земли
- (p0) — горизонтальный параллакс светила
Параллаксы планет и Солнца намного меньше, чем у Луны. Например, угол параллакса Солнца составляет всего несколько секунд дуги. Поскольку углы р0 малы, их синусы можно приблизительно заменить самими углами в радианах. Учитывая это, формулу можно переписать в виде:
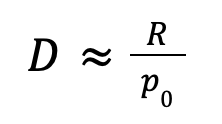
Где (p0) выражено в секундах дуги, а D — в километрах (если (R) в километрах) или в радиусах Земли.
2. Радиолокационный метод предполагает отправку мощного кратковременного импульса к небесному телу и последующий прием отраженного сигнала. Скорость распространения радиоволн равна скорости света в вакууме, т.е., () м/с. Исходя из этого, точное измерение времени, затраченного на прохождение сигнала до небесного тела и обратно, позволяет легко вычислить расстояние до него. Метод был предложен советскими физиками Л. И. Мандельштамом и Н. Д. Папалекси.
Этот метод обеспечивает высокую точность при определении расстояний до небесных тел Солнечной системы. Благодаря радиолокационным наблюдениям удалось уточнить расстояния до Луны, Венеры, Меркурия, Марса и Юпитера. Для успешных космических миссий крайне важно иметь точные значения астрономической единицы. Недавно, астрономическая единица была известна с точностью лишь до нескольких десятков тысяч километров. Однако благодаря радиолокационным наблюдениям Венеры, нам теперь известно более точное значение астрономической единицы:
1 а.е. = (149 597 868 ± 0,7) км.
Округленное значение астрономической единицы (149600000 км) соответствует параллаксу Солнца в (8,7940′).
3. Лазерная локация Луны была разработана сразу после появления мощных источников светового излучения — оптических квантовых генераторов, или лазеров. Этот метод аналогичен радиолокации, но обладает высокой точностью измерений. Оптическая локация позволяет определить расстояние между выбранными точками лунной и земной поверхности с точностью до сантиметров. Такая высокая точность имеет большое значение для решения задач космической геодезии, изучения движения земных континентов и развития космических исследований.













